Розглянемо випадок, коли виплати суми 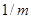 проводяться
проводяться 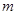 разів на рік, тобто в моменти часу
разів на рік, тобто в моменти часу 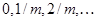 , поки людина
, поки людина 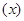 жива. Чиста одиночна премія такого аннуітету позначається
жива. Чиста одиночна премія такого аннуітету позначається 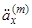 . По аналогії з (2.8) ми маємо
. По аналогії з (2.8) ми маємо
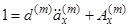 . (3.1)
. (3.1)
Звідси отримуємо
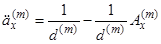 . (3.2)
. (3.2)
Це рівняння можна інтерпретувати так: Аннуітет життя, який виплачується 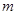 разів на рік, можна розглядати як різницю двох вічних аннуітетів, які починаються в моменти 0 і
разів на рік, можна розглядати як різницю двох вічних аннуітетів, які починаються в моменти 0 і 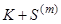 . Усереднюючи, отримаємо (3.2).
. Усереднюючи, отримаємо (3.2).
Для отримання виразу 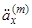 через
через 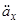 ми знову використаємо ситуацію А розділу 6 теми 2, звідки формула (3.10) теми 3 дозволяє виразити
ми знову використаємо ситуацію А розділу 6 теми 2, звідки формула (3.10) теми 3 дозволяє виразити 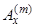 з (3.2) в термінах
з (3.2) в термінах 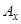 . Замінюючи потім
. Замінюючи потім 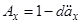 , ми можемо записати (3.2) у вигляді
, ми можемо записати (3.2) у вигляді
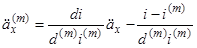 . (3.3)
. (3.3)
Ввівши позначення
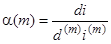 и
и 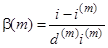 , (3.4)
, (3.4)
ми можемо записати (3.2) коротше
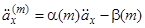 . (3.5)
. (3.5)
При 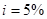 коефіцієнти
коефіцієнти 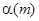 і
і 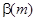 протабульовані нижче для
протабульовані нижче для 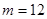 (помісячні платежі) і
(помісячні платежі) і 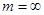 (неперервні платежі).
(неперервні платежі).
| M
| 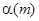
| 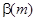
|
|
| 1.000197
| 0.46651
|
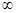
| 1.000198
| 0.50823
|
Як правило використовується апроксимація
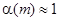 ,
, 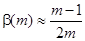 . (3.6)
. (3.6)
Ця апроксимація отримується з розкладу ряд Тейлора коефіцієнтів в околі 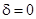 , тобто
, тобто
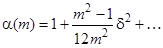 , (3.7)
, (3.7)
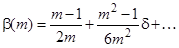 . (3.8)
. (3.8)
Очевидно, що ця апроксимація корисна тільки у випадку, коли сила відсотку достатньо мала.
Чиста одиночна премія термінового аннуітету життя pre-numerando з 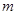 платежами щорічно може бути тепер виражена з використанням
платежами щорічно може бути тепер виражена з використанням 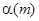 і
і 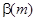 :
:
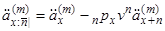
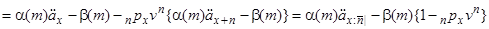 . (3.9)
. (3.9)
Чисту одиночну премію аннуітету post-numerando можна обчислити в термінах відповідних аннуітетів pre-numerando:
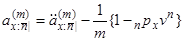 . (3.10)
. (3.10)
Повернемося до обчислення 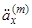 . Рівняння (2.8) і (3.1) дають точне співвідношення
. Рівняння (2.8) і (3.1) дають точне співвідношення
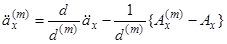 , (3.11)
, (3.11)
яке можна інтерпретувати так: Аннуітет життя з лівої сторони означає виплати суми 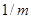 в моменти часу
в моменти часу 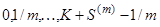 і дорівнює різниці двох термінових аннуітетів, перший з виплатами в моменти
і дорівнює різниці двох термінових аннуітетів, перший з виплатами в моменти 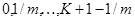 , а другий – в моменти
, а другий – в моменти 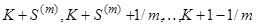 . Другий терміновий аннуітет в свою чергу може розглядатися як різниця двох нескінченних аннуітетів (які починаються в моменти
. Другий терміновий аннуітет в свою чергу може розглядатися як різниця двох нескінченних аннуітетів (які починаються в моменти 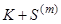 і
і 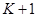 ). Перший терміновий аннуітет має таке ж поточне значення, як аннуітет pre-numerando з
). Перший терміновий аннуітет має таке ж поточне значення, як аннуітет pre-numerando з 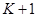 щорічними виплатами сумі
щорічними виплатами сумі 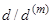 . Усереднюючи ці поточні значення, отримуємо (3.11).
. Усереднюючи ці поточні значення, отримуємо (3.11).
При ситуації А використання (3.10) дає
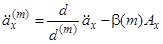 . (3.12)
. (3.12)
Ця формула має очевидну інтерпретацію, на відміну від математично еквівалентної формули (3.5).


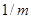 проводяться
проводяться 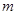 разів на рік, тобто в моменти часу
разів на рік, тобто в моменти часу 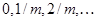 , поки людина
, поки людина 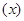 жива. Чиста одиночна премія такого аннуітету позначається
жива. Чиста одиночна премія такого аннуітету позначається 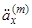 . По аналогії з (2.8) ми маємо
. По аналогії з (2.8) ми маємо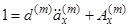 . (3.1)
. (3.1)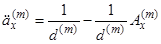 . (3.2)
. (3.2)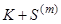 . Усереднюючи, отримаємо (3.2).
. Усереднюючи, отримаємо (3.2).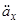 ми знову використаємо ситуацію А розділу 6 теми 2, звідки формула (3.10) теми 3 дозволяє виразити
ми знову використаємо ситуацію А розділу 6 теми 2, звідки формула (3.10) теми 3 дозволяє виразити 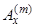 з (3.2) в термінах
з (3.2) в термінах 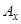 . Замінюючи потім
. Замінюючи потім 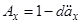 , ми можемо записати (3.2) у вигляді
, ми можемо записати (3.2) у вигляді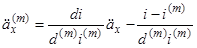 . (3.3)
. (3.3)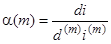 и
и 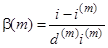 , (3.4)
, (3.4)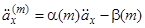 . (3.5)
. (3.5)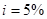 коефіцієнти
коефіцієнти 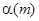 і
і 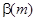 протабульовані нижче для
протабульовані нижче для 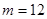 (помісячні платежі) і
(помісячні платежі) і 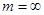 (неперервні платежі).
(неперервні платежі).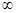
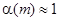 ,
, 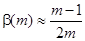 . (3.6)
. (3.6)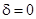 , тобто
, тобто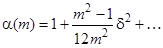 , (3.7)
, (3.7)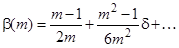 . (3.8)
. (3.8)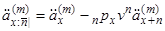
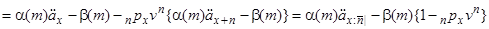 . (3.9)
. (3.9)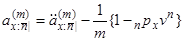 . (3.10)
. (3.10)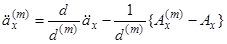 , (3.11)
, (3.11)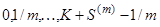 і дорівнює різниці двох термінових аннуітетів, перший з виплатами в моменти
і дорівнює різниці двох термінових аннуітетів, перший з виплатами в моменти 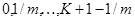 , а другий – в моменти
, а другий – в моменти 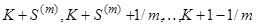 . Другий терміновий аннуітет в свою чергу може розглядатися як різниця двох нескінченних аннуітетів (які починаються в моменти
. Другий терміновий аннуітет в свою чергу може розглядатися як різниця двох нескінченних аннуітетів (які починаються в моменти 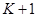 ). Перший терміновий аннуітет має таке ж поточне значення, як аннуітет pre-numerando з
). Перший терміновий аннуітет має таке ж поточне значення, як аннуітет pre-numerando з 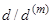 . Усереднюючи ці поточні значення, отримуємо (3.11).
. Усереднюючи ці поточні значення, отримуємо (3.11).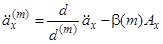 . (3.12)
. (3.12)