Сила смертності життя 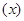 в момент досягнення віку
в момент досягнення віку 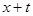 визначається співвідношенням
визначається співвідношенням
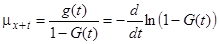 . (2.1)
. (2.1)
З (1.2) и (1.4) можна отримати інше співвідношення для ймовірності смерті в інтервалі між 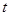 і
і 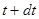 :
:
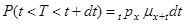 . (2.2)
. (2.2)
Середній час майбутнього життя для 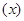 може бути записаний у вигляді
може бути записаний у вигляді
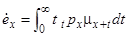 . (2.3)
. (2.3)
Апроксимація
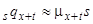 (2.4)
(2.4)
справедлива для малих значень 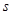 , що можна перевірити перестановкою значень
, що можна перевірити перестановкою значень 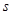 і
і 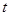 в (1.9) и порівняння результату з (2.2).
в (1.9) и порівняння результату з (2.2).
Силу смертності можна визначити також співвідношенням
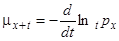 . (2.5)
. (2.5)
Інтегрування (2.5) дає
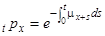 . (2.6)
. (2.6)
3. Аналітичний розподіл для майбутнього життя 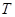
Будемо називати функцію 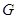 аналітичним або «математичним» розподілом ймовірності, якщо вона може бути виражена простою формулою.
аналітичним або «математичним» розподілом ймовірності, якщо вона може бути виражена простою формулою.
В минулому були намагання отримати універсальні аналітичні записи для 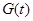 , виходячи з деяких базисних постулатів. Ці спроби на сьогодні вважаються щонайменше наївними.
, виходячи з деяких базисних постулатів. Ці спроби на сьогодні вважаються щонайменше наївними.
Аналітична формула має ту перевагу, що 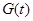 може бути безпосередньо підрахована через малу кількість числових параметрів. Статистичні методи більш доступні, коли невелика кількість параметрів підлягає оцінюванню.
може бути безпосередньо підрахована через малу кількість числових параметрів. Статистичні методи більш доступні, коли невелика кількість параметрів підлягає оцінюванню.
Аналітичні формули є також привабливими з точки зору теоретичних досліджень.
Наведемо деякі приклади аналітичних розподілів, які носять імена їх „творців”.
Де Муавр (De Moivre 1724) постулював існування максимального терміну життя 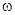 для людини і вважав, що
для людини і вважав, що 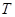 рівномірно розподілене між віком життя 0 і
рівномірно розподілене між віком життя 0 і 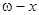 , тобто, що
, тобто, що 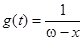 для
для 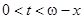 . Сила смертності тоді набуває вигляду
. Сила смертності тоді набуває вигляду
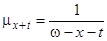 ,
, 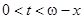 , (3.1)
, (3.1)
що є зростаючою функцією по 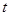 .
.
Гомпертц (Gompertz 1824) постулював, що сила смертності зростає по експоненті
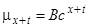 ,
, 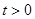 , (3.2)
, (3.2)
що краще описує смертність чим закон Де Муавра і в додаток не вимагає введення максимального віку життя  .
.
Закон (3.2) був узагальнений Мекхемом (Makeham 1860), який запропонував закон
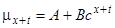 ,
, 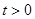 . (3.3)
. (3.3)
Закон смертності Мекхема додає константу, незалежну від віку компоненту 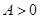 , до експоненціально зростаючої сили смертності (3.2).
, до експоненціально зростаючої сили смертності (3.2).
Спеціальні випадки законів смертності Гомпертца (при 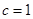 ) и Мекхема (при
) и Мекхема (при 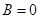 ) описують постійну силу смертності. Розподіл ймовірності для
) описують постійну силу смертності. Розподіл ймовірності для 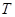 стає в цьому випадку експоненційним. Проте цей розподіл не відображає реальну картину смертності людей.
стає в цьому випадку експоненційним. Проте цей розподіл не відображає реальну картину смертності людей.
З (3.3) і (2.6), поклавши 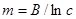 , імовірність виживання в моделі Мекхема можна записати у вигляді
, імовірність виживання в моделі Мекхема можна записати у вигляді
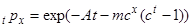 , (3.4)
, (3.4)
Вейбул (Weibull 1939) запропонував представляти силу смертності степеневою функцією від 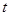 , а не експоненційною
, а не експоненційною
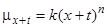 , (3.5)
, (3.5)
с фіксованими параметрами 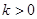 и
и 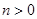 . Імовірність виживання тоді запишеться
. Імовірність виживання тоді запишеться
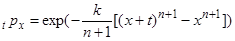 . (3.6)
. (3.6)
4. Вкорочений час майбутнього життя для 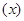
Повертаючись до загальної моделі, яка була запропонована в розділах 1 і 2, визначимо випадкові змінні 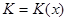 ,
, 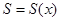 ,
, 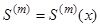 , які тісно пов’язані з випадковою змінною
, які тісно пов’язані з випадковою змінною 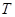 .
.
Назвемо 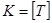 , кількість повних років, які прожиті життям
, кількість повних років, які прожиті життям 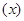 у майбутньому, вкороченим часом майбутнього життя для
у майбутньому, вкороченим часом майбутнього життя для 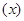 . Розподіл ймовірності цілочисельної випадкової змінної
. Розподіл ймовірності цілочисельної випадкової змінної 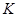 визначається формулою
визначається формулою
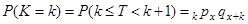 (4.1)
(4.1)
для 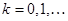 . Середнє значення
. Середнє значення 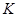 називається середнім вкороченим часом майбутнього життя для
називається середнім вкороченим часом майбутнього життя для 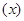 і позначається
і позначається 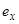 . Тому
. Тому
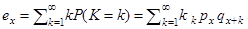 (4.2)
(4.2)
або
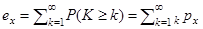 . (4.3)
. (4.3)
Використання середнього вкороченого часу життя має переваги, оскільки (4.1) і (4.2) легше оцінити, чим (1.11) і (2.3). Іншою перевагою є те, що для знаходження 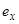 достатньо знати розподіл
достатньо знати розподіл 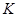 .
.
Нехай 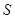 - та частина року смерті
- та частина року смерті 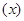 , протягом якої він живий, тобто
, протягом якої він живий, тобто
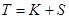 . (4.4)
. (4.4)
Випадкова змінна 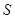 має неперервний розподіл між 0 і 1. Наближуючи її середнє значення величиною ½, ми знайдемо з (4.4) апроксимацію
має неперервний розподіл між 0 і 1. Наближуючи її середнє значення величиною ½, ми знайдемо з (4.4) апроксимацію
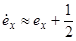 , (4.5)
, (4.5)
яка може бути використана на практиці для середнього часу майбутнього життя для 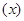 .
.
Нехай 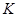 і
і 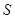 - незалежні випадкові змінні, так що умовний розподіл для
- незалежні випадкові змінні, так що умовний розподіл для 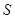 , при заданому
, при заданому 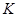 , не залежить від
, не залежить від 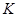 ; тоді
; тоді
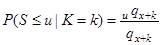 (4.6)
(4.6)
не залежить від аргументу 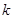 , отже можна записати, що
, отже можна записати, що
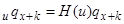 (4.7)
(4.7)
для 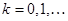 ,
, 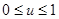 і деякої функції
і деякої функції 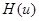 .
.
Якщо обрати 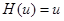 (рівномірний розподіл між 0 і 1), то апроксимація (4.5) стає точною. Більше того, використовуючи (4.6) і постульовану незалежність, дисперсію
(рівномірний розподіл між 0 і 1), то апроксимація (4.5) стає точною. Більше того, використовуючи (4.6) і постульовану незалежність, дисперсію 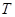 можна записати у вигляді
можна записати у вигляді
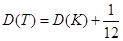 або
або 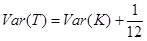 . (4.8)
. (4.8)
Для додатних цілих 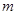 визначимо випадкову змінну
визначимо випадкову змінну
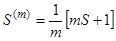 . (4.9)
. (4.9)
Таким чином,  отримується з
отримується з 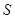 округленням до наступного більшого кратного
округленням до наступного більшого кратного 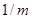 . Розподіл
. Розподіл  зосереджений в точках
зосереджений в точках 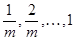 . Зауважимо, що незалежність між
. Зауважимо, що незалежність між 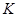 і
і 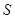 веде за собою незалежність між
веде за собою незалежність між 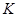 і
і  . Крім цього, якщо
. Крім цього, якщо 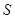 рівномірно розподілена між 0 і 1, то
рівномірно розподілена між 0 і 1, то  має дискретний рівномірний розподіл.
має дискретний рівномірний розподіл.


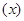 в момент досягнення віку
в момент досягнення віку 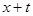 визначається співвідношенням
визначається співвідношенням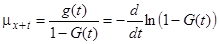 . (2.1)
. (2.1)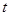 і
і 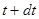 :
: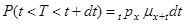 . (2.2)
. (2.2)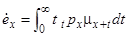 . (2.3)
. (2.3)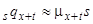 (2.4)
(2.4)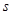 , що можна перевірити перестановкою значень
, що можна перевірити перестановкою значень 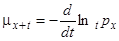 . (2.5)
. (2.5)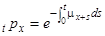 . (2.6)
. (2.6)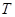
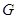 аналітичним або «математичним» розподілом ймовірності, якщо вона може бути виражена простою формулою.
аналітичним або «математичним» розподілом ймовірності, якщо вона може бути виражена простою формулою.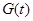 , виходячи з деяких базисних постулатів. Ці спроби на сьогодні вважаються щонайменше наївними.
, виходячи з деяких базисних постулатів. Ці спроби на сьогодні вважаються щонайменше наївними.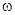 для людини і вважав, що
для людини і вважав, що 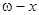 , тобто, що
, тобто, що 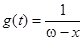 для
для 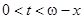 . Сила смертності тоді набуває вигляду
. Сила смертності тоді набуває вигляду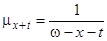 ,
, 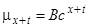 ,
, 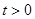 , (3.2)
, (3.2)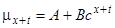 ,
, 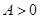 , до експоненціально зростаючої сили смертності (3.2).
, до експоненціально зростаючої сили смертності (3.2).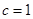 ) и Мекхема (при
) и Мекхема (при 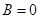 ) описують постійну силу смертності. Розподіл ймовірності для
) описують постійну силу смертності. Розподіл ймовірності для 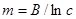 , імовірність виживання в моделі Мекхема можна записати у вигляді
, імовірність виживання в моделі Мекхема можна записати у вигляді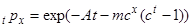 , (3.4)
, (3.4)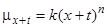 , (3.5)
, (3.5)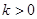 и
и 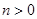 . Імовірність виживання тоді запишеться
. Імовірність виживання тоді запишеться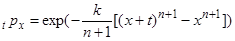 . (3.6)
. (3.6)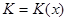 ,
, 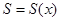 ,
, 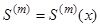 , які тісно пов’язані з випадковою змінною
, які тісно пов’язані з випадковою змінною 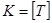 , кількість повних років, які прожиті життям
, кількість повних років, які прожиті життям 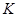 визначається формулою
визначається формулою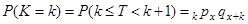 (4.1)
(4.1)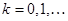 . Середнє значення
. Середнє значення 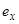 . Тому
. Тому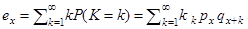 (4.2)
(4.2)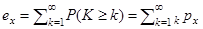 . (4.3)
. (4.3)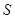 - та частина року смерті
- та частина року смерті 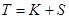 . (4.4)
. (4.4)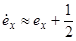 , (4.5)
, (4.5)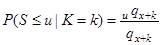 (4.6)
(4.6)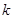 , отже можна записати, що
, отже можна записати, що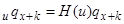 (4.7)
(4.7)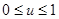 і деякої функції
і деякої функції 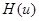 .
.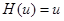 (рівномірний розподіл між 0 і 1), то апроксимація (4.5) стає точною. Більше того, використовуючи (4.6) і постульовану незалежність, дисперсію
(рівномірний розподіл між 0 і 1), то апроксимація (4.5) стає точною. Більше того, використовуючи (4.6) і постульовану незалежність, дисперсію 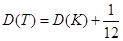 або
або 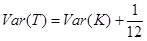 . (4.8)
. (4.8)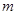 визначимо випадкову змінну
визначимо випадкову змінну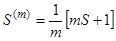 . (4.9)
. (4.9) отримується з
отримується з 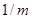 . Розподіл
. Розподіл 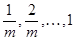 . Зауважимо, що незалежність між
. Зауважимо, що незалежність між